Perma-clipse | PhysOx

Perma-clipse: Prerequisites

You should be familiar with the following topics:

Geometry
Vectors
Circular motion (A Level)
Gravitation (A Level)

Introduction

Firstly we'd like to start off by saying, if you have not seen a solar eclipse, it should be on your bucket list!

In the case that you do get a chance to see one, whether partial, annular or total (the difference will be explained later on), make sure to never directly look at the sun. Despite the perceived decrease in brightness, it is still bright enough to permanently damage your eyes. Proper safety precautions should be taken [4].

Almost all of you will know or have at least heard of what an eclipse is; just for the sake of completeness we will still quickly overview the topic. For those who are also visual and auditory learners we recommend this video [1] on the topic; of course only watch it after you finish reading this article! Now let's get started!

There are two types of eclipses. These can each be split into sub-groups: lunar and solar.

Lunar Eclipses

In general, if we have an extended light source (a light source that does not solely originate from a single point) and an opaque object that obscures its light to form a shadow, the shadow will have three regions: the umbra, penumbra and antumbra [5]. These regions are depicted in figure 1. The umbra is the innermost region of a shadow. For an opaque object, no light from the source reaches this region. The penumbra is the region of the shadow where only part of the source is obscured. A wider definition of the penumbra would be the region of a shadow where the source is partially or fully obscured making the previously mentioned umbra and the to-be-discussed antumbra subsets of the penumbra. We shall use the former rather than the latter as a definition. For an extended source, the transition between the two regions is smooth, whereas for a point source this transition is more "sharp". The antumbra is the region of space from which the opaque object is observed to lie entirely within the extended light source (figure 1). This region of the shadow becomes visible if you move away far enough from the opaque object and appears lighter than the penumbra. We can see why this is the case by considering the extended source in figure 1 as two point point sources S1 and S2. The penumbra in the upper region will not see S2 and and the penumbra in the lower region will not see S1. The antumbra will partially or fully see both S1 and S2.

In the case of a lunar eclipse, the role of the extended source is played by the sun and the 'opaque' object is played by the Earth. As mentioned before, there are three main types of eclipses: totality, penumbral and partial. Partial can be split into two further groups for a lunar eclipse: partial and partial penumbral. Lunar totality occurs when the moon lies within the umbra of the Earth's shadow. Note that we used opaque in quotation marks above because the Earth is not opaque; it has an atmosphere that lets some light through. Hence, rather than the Moon appearing black in this region, it appears red due to Rayleigh scattering, causing red light to be diffracted into the umbral region [6]. A penumbral lunar eclipse occurs if the moon passes through the penumbral region of the shadow. The lunar partial eclipse is when the moon lies between the penumbra and umbra, where as the partial penumbral lunar eclipse occurs when the moon lies between the no-shadow and penumbral regions. Figure 2 provides a visual depiction of all the cases described above. For photos and more information [2].

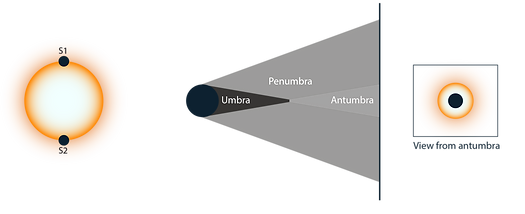
Fig 1

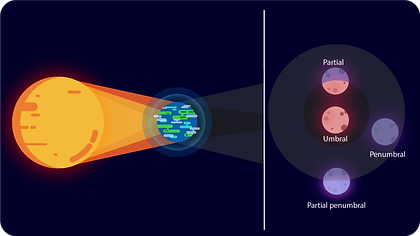
Fig 2

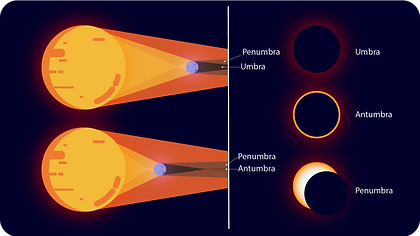
Fig 3

Solar Eclipses

A solar eclipse occurs when the Moon positions itself in such a way that its shadow falls on the Earth. There are three types of solar eclipses. The first of these which we will discuss, is a total solar eclipse or solar totality. Unlike lunar totality, solar totality can only be seen by the few people on the Earth that lie within the umbra of the moon's shadow. Only about 0.5% of the Earth's surface can view a total eclipse and the only reason we can see a total solar eclipse at all is due to moon perfectly covering the sun from the vantage point of the Earth! This happens as the angular diameter of the Sun and the Moon are equal for an observer on the surface of the Earth; the Moon is roughly 400 times smaller than the Sun but also 400 times further away! If you don't know what angular diameter is do not worry, we will define it in the theory section below as we will need to know formally what it is to do our calculations. Solar totality is often considered the most spectacular eclipse to experience as you can see the sun's atmosphere from the Earth with the naked eye - super cool!

For the observers on Earth lying outside the umbra but still within the penumbra, they will experience a partial solar eclipse where the moon covers only part of the sun as it passes by. What this looks like can be seen illustratively in figure 3. For an image of what this looks like in real life, see [3].

In figure 3 you can also see a third type of solar eclipse. This third type occurs due to the fact that the moon's orbit is not perfectly circular but has some eccentricity to it. When the moon is at its furthest point from the Earth, it appears smaller than the Sun from the line of sight of observers on the Earth. That is to say that we lie within the antumbra cast by the Moon. When this occurs, we see an annular solar eclipse. The Moon looks like it has a ring of fire around it!

Fig 4

Are eclipses rare?

After reading the information above, some of you may wonder why we don't see an eclipse at least once every 28 days. For an eclipse to happen, the Earth, Moon and Sun need to line up. If the plane of the moon's orbit coincided with Earth-Sun plane, then eclipses would actually occur once every 28 days, but this is not the case. The angle between the normals of the two planes are roughly 5 degrees (see figure 4). This may seem small but it is large enough such that, at the distance the moon is from the Earth, the celestial objects' shadows can completely miss each other. This creates a another condition for an eclipse to occur; the line of intersection between the two planes (visually depicted in figure 4 as the line between the moon) must coincide with the line connecting the Sun and the Earth. This happens twice a year [7]. An animation of this can be seen in figure 5. This 5 degree tilt is also what causes there to be the different types of lunar eclipse. If the tilt did not exist, the Moon would always transition through each of the eclipse types rather than only one occurring at a time.

Some might still say "Solar eclipses seem to occur less frequently than a lunar eclipse". However, it only feels this way due to solar eclipses only being viewable by a small percent (0.5%) of the Earth's surface [7] whereas for lunar eclipses, everyone on the dark side of the planet can view it.

fig 5: Alignment

fig 6: w_s = 1.6 w_E

fig 7: w_s = w_E

Theory

Now that we are all hopefully all on the same page, we can discuss why the title of this post is named perma-clipse. Imagine that you are a crazy scientist (like Gru or Dr Nefario in Despicable Me) and want to create a permanent eclipse: how would you go about doing this? We will conduct a little thought experiment below! The set up is pretty simple (figure 8).

Fig 8

Here is how we will approach this problem:

Calculate the angular velocity of the satellite
Calculate its orbital radius
Find its angular diameter

Angular velocity

Figure 8 diagrammatically describes the evolution of a Sun-Moon-Earth-like system. The variable 'a' is the initial angle in respect to the horizontal at time 't = 0'. For the general case, the angle between the Sun-Moon vector and the Sun-Earth vector, phi, will evolve in time as the system evolves (see figure 6) but for certain pairs of values of (w_E,w_s) phi actually becomes fixed; from the point of view of Earth, the satellite's position in the sky will be the same at the same time of the day. For values of 'a' equal to pi or zero, this would correspond to a solar or lunar eclipse happening everyday (given that the angle between the Earth-Moon and Earth-Sun plane is zero).

To find the pairs of values for the angular momentum, we fix the value of phi by saying that the satellite and Earth have the same angular velocity around the sun. To quickly see why we can say this, we use linear motion as an analogy. We define displacement as the angle between the vectors of the two bodies and the angular velocity is to rotational motion what linear velocity is to linear motion. Just like the displacement between two bodies does not change if they have the same linear velocity, the angle between two objects rotating about the same point also stays constant if they have the same angular velocity. For the simplest case, algebraically we consider case where 'a = 0'. Our approach will be to write down the general vector equation for the system (equation 1) and equate it to the vector for the case where we have fixed the value of phi (equation 2). We leave 'w_E' to take some arbitrary value hence we only have to find one variable, 'w_s'. Since we only have one unknown, we can deal with one component of the vector ('n' unknowns require 'n' equations to solve for them).

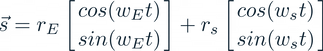
(1)

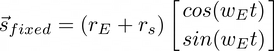
(2)

To find the value of 'w_s' for a given 'w_E', we equate the x-component of each of the vectors and solve for 'w_s' as mentioned above; the result pops out almost immediately:

(3)

(4)

(5)

Equation 3 immediately results in equation 4, in which we see that for phi to be fixed for our chosen value of 'a=0', the angular velocity of the satellite around Earth should be equal to the angular velocity of the Earth around the sun. The case of 'a = pi' gives the same result (graphically depicted in figure 7) and is left as an exercise to the reader.

Orbital radius

Now that we have determined our angular velocity, we need to determine the orbital radius to achieve such an angular velocity. For this we will dip out feet into some orbital mechanics! We will assume a circular orbit such that we only deal with circular motion.

For an object to undergo circular motion around another body under the gravitational force, this force must be equal to the centripetal force (equation 6). For this calculation we assume that the effect of the gravitational force on the satellite due to the Sun is negligible and hence we ignore it.

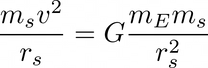
(6)

(7)

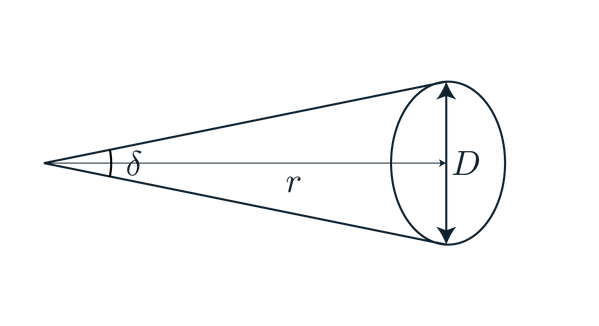
Fig 9

To arrive at equation 7 and the equation for the orbital radius from equation 6, we have used equation 5 and the result of equation 4. 'G' in the equations above is the gravitational constant. For this given orbital radius we need to also make sure that we have the correct angular diameter such that for the case of a solar eclipse ('a=pi'), we can achieve daily totality if we so desire.

Angular diameter

We have used the word angular diameter before, but here we define it more rigorously. Definition: the angular diameter or apparent size is a quantity describing the measured size of an circle from a given point of reference. From figure 9 we derive the equation for the angular diameter of such a circle (equation 8).

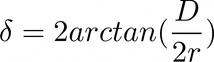
(8)

We stated above that we are looking to produce totality; for this to occur, we need the angular diameters of the satellite and Sun to be equal from the point of view of the Earth. We capture this in equation 9 and hence solve for the diameter of the projected area of our satellite, which we assume to be spherical. Definition: the projected area is the measured area of a three dimensional object that has been projected onto an arbitrary plane. The projected area of a sphere is a circle which has a diameter equal to the diameter of the sphere. To arrive at equation 10 from equation 9, we use equation 7.

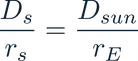
(9)

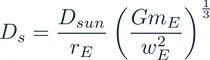
(10)

Fig 10

'D_s' and 'D_sun' are the diameter of the satellite and Sun respectively. We have now calculated all the quantities needed to construct a daily eclipse; equation 4 tells us what angular velocity to use, equation 7 gives us the orbital radius and equation 10, the diameter of the satellite. Let's now apply the equations we have derived.

If we wanted the Moon to produce a daily eclipse, what would we need to alter to achieve this ?

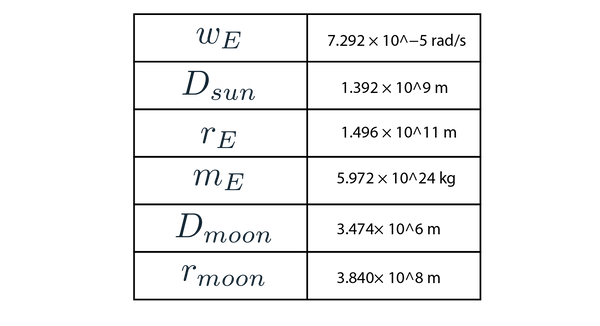
Note the values given in the table are averages, as the true values vary due to things such as eccentricity (elliptical/tilted orbit rather than the perfect circular orbit we assumed in our calculations). Sources for these true values can be found in the references section. Using the data in the table we find that the gif at the start of the theory section is inaccurate (!), we actually need to enlarge the moon by 12.9% and increase its orbital radius by 9.80% (note again that we assumed that in this case, the angle of the Earth-Moon plane in relation to the Earth-Sun plane is zero).

Perma-clipse: Prerequisites

Introduction

Theory

References